.md .pdf

repository open issue

Contents

Aufgabenstellung

Cäsar Chiffre

Die Verschlüsselung basiert auf der Cäsar-Chiffre. Sie ist eine der einfachsten und am weitesten verbreiteten Verschlüsselungstechniken. Das Alphabet wird um \(k\) verschoben, wodurch verschiedene Buchstaben miteinander verbunden werden. Das bedeutet, dass bei einer gegebenen Chiffre die Buchstaben immer einander entsprechen.

Important

Die Cäsar-Chiffre bietet heute im Wesentlichen keine Kommunikationssicherheit mehr.

Fig. 52 Cäsar-Chiffre mit \(k = 3\) Quelle: Wikipedia

Aufgaben

Als erstes wir als Beispiel ein Cäsar Chiffrierung implementiert. Dies wird in mehreren Schritten durchgeführt:

1. Kontrollieren ob der Character ein Buchstabe ist

2. Suchen des Index des Buchstaben

3. Inkrementieren oder dekrementieren des Indexes

4. Suchen des neuen Buchstaben

Aufgabe 1 - Lesen eines Strings

Versuche den Buchstaben "H" herauszulesen

# TODO 1

Aufgabe 2 - Kontrollieren ob der Character ein Buchstabe ist

Es ist zu kontrollieren ob der characterim alphabet vorkommt. Wir werden dies in der Funktion isLetter() implementieren.

# TODO 2

Aufgabe 3 - Suchen des Index der Buchstaben

Finde den index des characters in der liste alphabet Wir werden dies in der Funktion idxOfLetter() implementieren

# TODO 3

Aufgabe 4 - Inkrementieren oder dekrementieren des Indexes

Der k Wert kann positiv sowie Negativ sein. Die Spezialfälle <0 und >25 sollten auch in Betracht gezogen werden Wir werden dies in der Funktion incrementIndex() implementieren

# TODO 4

Aufgabe 5 - Cäsar Chiffirerung

Implementieren sie die Enkodierung in der Funktion cesarEncoding() und testen Sie diese.

# TODO 5

Important

Gratulation Sie haben soeben eine Cäsar Chiffriermaschine entwickelt

Theorie Enigma

Bezeichnungen

• Steckerbrett - der Steckbrett vor der Maschine, kann zwei verschiedene Buchstaben miteinander verbinden. Dies ist eine zusätzliche Verwirrungsebene

• Rotoren - zwischen dem Steckbrett und dem Reflektor können die drei Rotoren links, mittig und rechts in eine bestimmte Position gebracht werden, um ein andere Vermischung zu erreichen

• Reflektor - Der Reflektor empfängt die Signale des linken Rotors und sendet sie an ihn zurück, die Reflektor-Verschlüsselung kann nicht verändert werden. Er ermöglicht es der Maschine, zu kodieren und zu dekodieren, ohne irgendwelche Einstellungen zu ändern.

Algorithmus

Die Enigma-Maschine funktioniert auf ähnliche Weise wit der Cesar Algorithmus aber mit einer komplexeren Struktur.

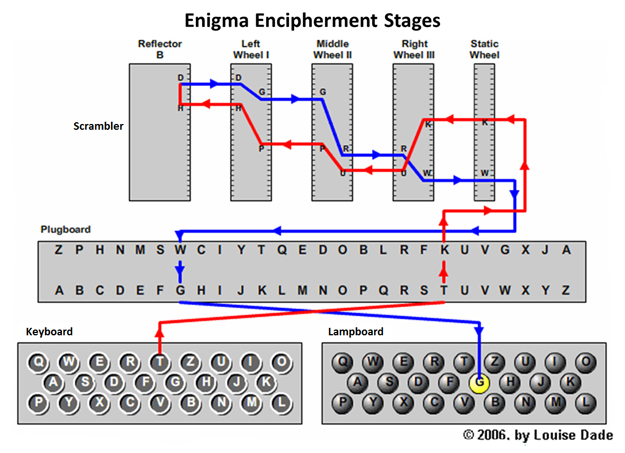
Fig. 53 Enigma-Diagramm Quelle: Louise Dade

Einstellung

Um zu entschlüsseln, was eine andere Maschine verschlüsselt hat, muss Folgendes zutreffen:

• Die gleiche Maschine mit der gleichen Anzahl und den gleichen Typen von Rotoren und Reflektoren.

• Die Plugboard-Einstellungen müssen die gleichen sein.

• Gleiche Startposition der Rotoren

All diese Informationen wurden täglich geändert, die genauen Einstellungen waren in einem monatlich herausgegebenen “Codeblatt” zu finden.

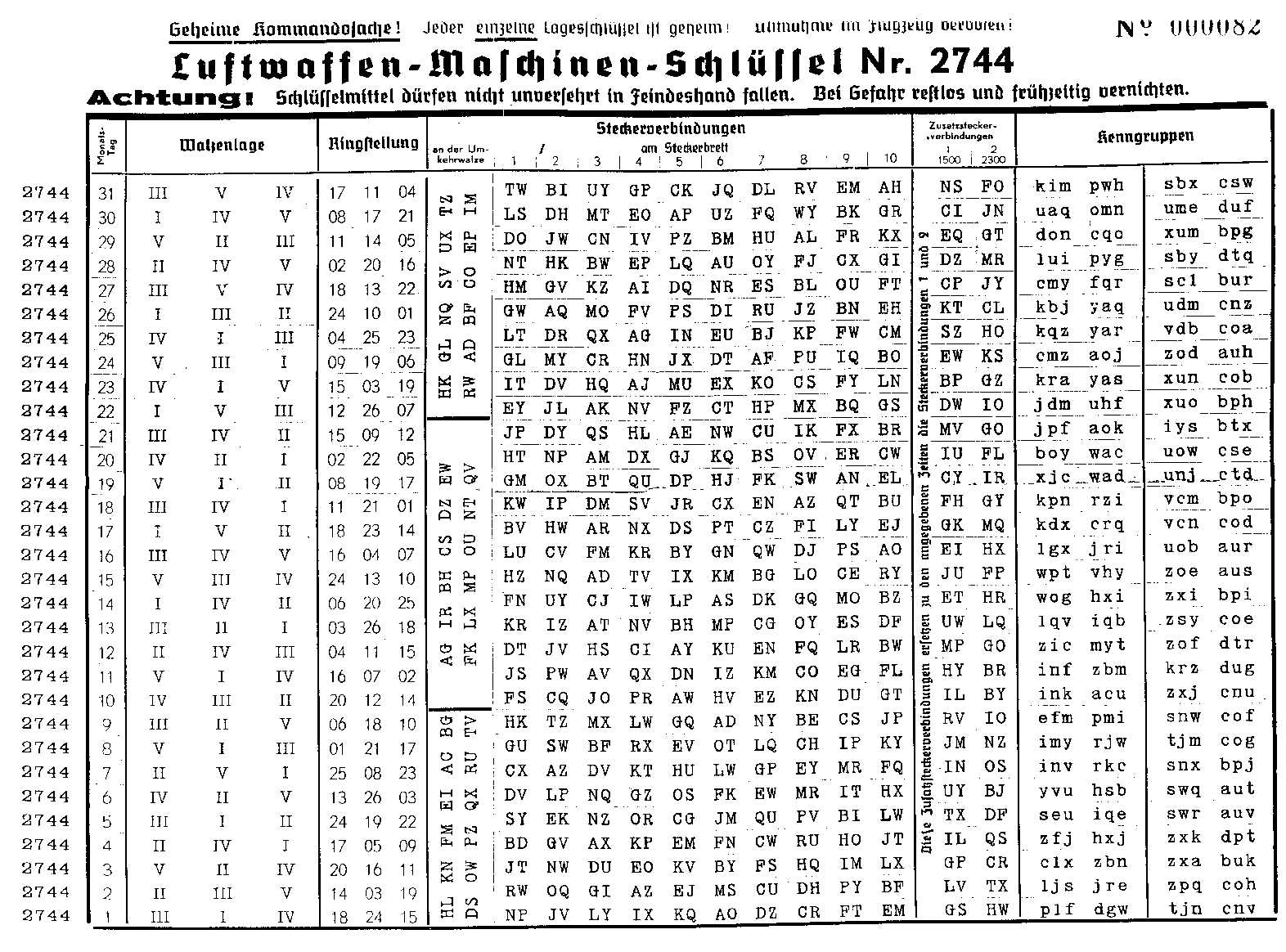
Fig. 54 Codesheet WWII Source: Nazis

Rotor- und Reflektortypen

Während der Zeit, in der die Enigma verwendet wurde, gab es viele verschiedene Versionen mit unterschiedlichen Rotoren und Reflektoren. Von insgesamt 5 Möglichen Rotoren mussten jeden morgen 3 andere benutzt werden. Die Reflektoren änderten grundsätzlich nicht.

Schlüssel	Typ	Einrichtung	Verwendung
etw	Rotor ETW	ABCDEFGHIJKLMNOPQRSTUVWXYZ	Enigma I
i	Rotor I	EKMFLGDQVZNTOWYHXUSPAIBRCJ	1930 Enigma I
ii	Rotor II	AJDKSIRUXBLHWTMCQGZNPYFVOE	1930 Enigma I
iii	Rotor III	BDFHJLCPRTXVZNYEIWGAKMUSQO	1930 Enigma I
iv	Rotor IV	ESOVPZJAYQUIRHXLNFTGKDCMWB	December 1938 M3 Army
v	Rotor V	VZBRGITYUPSDNHLXAWMJQOFECK	December 1938 M3 Army
vi	Rotor VI	JPGVOUMFYQBENHZRDKASXLICTW	1939 M3 & M4 Naval (FEB 1942)
vii	Rotor VII	NZJHGRCXMYSWBOUFAIVLPEKQDT	1939 M3 & M4 Naval (FEB 1942)
viii	Rotor VIII	FKQHTLXOCBJSPDZRAMEWNIUYGV	1939 M3 & M4 Naval (FEB 1942)
a	Reflector A	EJMZALYXVBWFCRQUONTSPIKHGD
b	Reflector B	YRUHQSLDPXNGOKMIEBFZCWVJAT
c	Reflector C	FVPJIAOYEDRZXWGCTKUQSBNMHL
custom	Custom	as given by the user

Codegrösse

Die Codegrösse gibt die Anzahl an Verschlüsselungsmöglichkeiten an.

Die Formel der Gesamten Codemöglichkeiten ist wiefolgt:

\[(5*4*3)*26^3*\frac{26!}{6!*10!*2^{10}} = 158 962 555 247 826 360 000\]

Diese Formel wird untenstehend aufgesplitet und erklärt.

Walzenauswahl

Aus 5 Walzen werden 3 ausgewählt und beliebig platziert.

\(5*4*3 = 60\) WalzenKombinationsmöglichkeiten

Startposition der Walzen

3 Walzen von je 26 Möglichen Positionen

\(26^3 = 17576\) Walzen Startpositionen

Steckerbrett Kombinationen

Hier können jeweils 2 Buchstaben miteinander verbunden werden. Total waren 10 Steckerverbindungen möglich. 6 waren also unbenutzt

• \(26!\) - Möglichen Kombinationsmöglichkeiten des Alphabets

• \(6!\) - 6 Steckerverbindungen blieben unbenutzt

• \(10!\) - Es gibt nur 10 Steckverbindungen durchzuführen

• \(2^{10}\) - Verbinden A <=> Z ist das gleiche wie Z <=> A

\[ \frac{26!}{6!*10!*2^{10}} = 150 738 274 937 250\]

Demonstration

Als Demo können Sie sich das folgende Youtube Video anschauen.

Enigma Demonstration

Vorbereitung

Noch bevor Code geschrieben wurde, wurde ein Klassendiagram erstellt. Die Idee ist eine Klasse der EnigmaMaschine zu erstellen welche mehrere Scrambler-Objekte besitzt. Ein Steckerbrett, die Rotoren aber auch der Reflektor funktionieren im Prinzip das Sie verschiedene Buchstaben miteinander verbinden bzw vermischen (scramble). Obwohl Sie mechanisch anders aufgebaut sind ist die Funktionsweise die selbe.

Fig. 55 EnigmaMachine Datenfluss

Das Klassendiagram der Applikation:

Fig. 56 Enigma Klassendiagramm

Scrambler

Als erstes werden wir die Klasse Scrambler schreiben.

Fig. 57 Scrambler Klassendiagramm

Important

Mit hilfe print() Befehlen müsst Ihr euren Code selber debuggen.

Aufgabe 6 - Typen Schlüssel

Der Typenschlüssel wird als String angegeben. Die möglichen Werte sind: "etw", "i", "ii", "iii", "iv", "v", "vi", "vii", "viii" für die Rotoren sowie "a", "b", "c" für die Reflekotren. Der Scrambler sollte auch folgende Werte al gültig erkennen können.

• Grossbuchstaben - "I", "II", ViIi

• Bindestriche - "v-iii", e-t-w

• Leerschläge - "v iii", "e t w"

• Unterstriche - "v_iii", e_t_w

• Kombinationen der obigen Fehler.

self.type_key sollte ein bereinigter String beinhalten

# TODO 6

Aufgabe 7 - String zu Array

Die Konfiguration wird mit String in folgender Form ausgedrückt:

str_config = "EKMFLGDQVZNTOWYHXUSPAIBRCJ"

Dieser String muss verändert werden in Form eines Array’s

config = ["E","K","M","F","L","G","D","Q","V","Z","N","T","O","W","Y","H","X","U","S","P","A","I","B","R","C","J"]

# TODO 7

Aufgabe 8 - Rotierender String

Bei jedem Schritt einer Rotors muss der String nach links rotiert werden.

• Aus "Test" wird "estT" falls um n=1 geschoben werden soll.

• Aus "Test" wird "stTe" falls um n=2 geschoben werden soll.

# TODO 8

Enigma Machine

Das Klasse Scrambler ist nun geschieben und getestet.

Fig. 58 EnigmaMachine Klassendiagramm

Aufgabe 9 - Steckerbrett

Die Konfiguration des Steckerbrettes wird folgendermassen gegeben.

self.plugboard_config = ["AZ", "BY", "CX", "DW", "EV", "FU", "GT", "HS", "IR", "JQ", "KP", "LO", "MN"]

Diese Konfiguration muss in die type_key Form übertragen werden. Im obigem Beispiel:

ZYXWVUTSRQPONMLKJIHGFEDCBA

Damit dem Alphabet "ABCDEFGHIJKLMNOPQRSTUVWXYZ" im obigen Beispiel A <-> Z gegenübersteht sowie B <-> Y etc.

Important

Ein Python String kann nicht verändert werden, der String muss neu erstellt werden.

string    = "ABC"
string[0] = "D"               # Funktioniert nicht
string    = "D" + string[1:]  # "DBC"

# TODO 9

Aufgabe 10 - Enigma Setup

Die Enigma Setup sollte angezeigt werden können damit man dieser weitergeben kann.

Die Funktion printEnigmaSetup() sollte der folgende oder änhlicher Ausgabe vorweisen. Es ist wichtig zu erwähnen das unsere Enigma Maschine eine beliebige Anzahl Rotoren vorweisen kann.

Enigma Setup
============

* Rotor 0
  - Type      : i
  - Key       : USPAIBRCJEKMFLGDQVZNTOWYHX
  - StartPos  : 17
* Rotor 1
  - Type      : iii
  - Key       : SQOBDFHJLCPRTXVZNYEIWGAKMU
  - StartPos  : 23
* Rotor 2
  - Type      : iv
  - Key       : RHXLNFTGKDCMWBESOVPZJAYQUI
  - StartPos  : 12
* Reflector
  - Type      : a
* Plugboard
  - Key       : ['AZ', 'BY', 'CX', 'DW', 'EV', 'FU', 'GT', 'HS', 'IR', 'JQ', 'KP', 'LO', 'MN']

Benutzt hierzu die folgenden Variablen der Scrambler-Objekte:

self.nb_rotors
self.rotors[i].type_key
self.rotors[i].key
self.rotors[i].startpos
self.reflector.type_key
self.reflector.key
self.reflector.startpos
self.plugboard_config

# TODO 10

Aufgabe 11 - Enkodierung des Charakter

Jeden Charakter muss alle Scrambler durchlaufen. Der Charakter wurde bereits als Position im Alphabeth decodiert num. Anhand des existierenden Beispieles muss dieser Wert nun jeden Scrambler durchlaufen. z.B das Steckerbrett:

 num = self.plugboard.passthrough(num)

Es ist zu beachten das es zum durchlaufen in die eine Richtung die Funktion passthrough() und in die andere Richtung passthroughRev() benötigt.

# TODO 11

Verschlüsselte Nachrichten Übermitteln

Als letzte Aufgabe schickt eurem Studienkollegen einen verschlüsselte Nachricht. Hierzu müsst Ihr Ihnen die verschlüsselte Nachricht aber auch das Setup übermitteln.

1. Bereitet eine Nachricht und eine Enigma Konfiguration vor

2. Verschüsselt die Nachricht

3. Gebt eurem Kollegen die Nachricht sowie die Konfigurationsparameter

4. Dekodiert die Nachricht welche Ihr von euerem Kollegen erhalten habt

previous

Enigma Machine

next

Programmierung