Prime numbers with Eratosthenes sieve
Contents
Prime numbers with Eratosthenes sieve¶
Sieve of Eratosthenes is an ancien greek algorithm for finding all prime numbers up to any given limit.
A prime number is natural number that has exactly two distinct natural numbers divisors; the number 1 and itself.
The first prime numbers are
Solution¶
To find all the prime numbers less than or equal to a given integer \(n\) by Eratosthenes’ method:
Create a list of consecutive integers from \(2\) through \(n\): \((2, 3, 4, ..., n)\).
Initially, let \(p\) equal 2, the smallest prime number.
Enumerate the multiples of \(p\) by counting in increments of \(p\) from \(2p\) to \(n\), and mark them in the list (these will be \(2p, 3p, 4p, ...;\) the \(p\) itself should not be marked).
Find the smallest number in the list greater than \(p\) that is not marked. If there was no such number, stop. Otherwise, let \(p\) now equal this new number (which is the next prime), and repeat from step 3.
When the algorithm terminates, the numbers remaining not marked in the list are all the primes below \(n\).
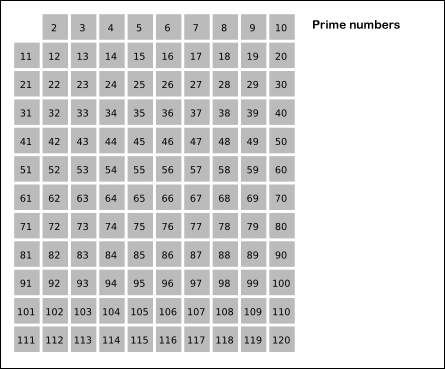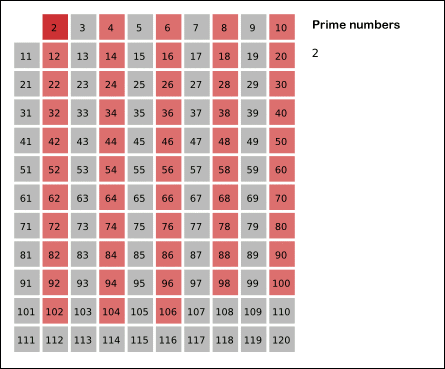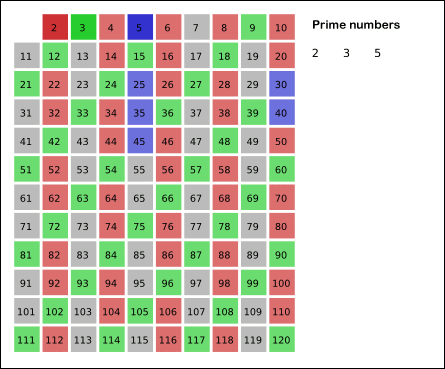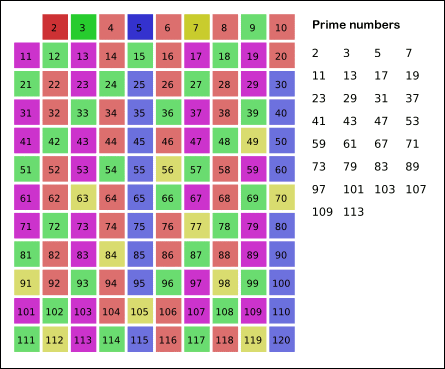
Fig. 8 Animation Sieve of Eratosthenes Source: Wikipedia¶
Imports¶
import numpy as np
Algorithm¶
def seive_of_eratosthenes(n: int = 2):
"""Algorithm to get all Prime numbers up to the value n
Args:
n (int, optional): End number for the prime calculations. Defaults to 2.
Returns:
list: list of all primenumber upto n
"""
# create empty array
_is_prime = [True for i in range(n + 1)]
# 0 and 1 are not primes
_is_prime[0] = _is_prime[1] = False
p = 2
while (p * p <= n):
# If prime[p] is not changed, then it is a prime
if (_is_prime[p] == True):
# Update all multiples of p
for i in range(p ** 2, n + 1, p):
_is_prime[i] = False
p += 1
return _is_prime
def print_primenumbers(is_prime: list):
"""Print all prime numbers indicated on a boolean list
Args:
is_prime (list): list of boolean indicating of the number is a prime
"""
print("Following are the prime numbers smaller than {}".format(len(is_prime)))
for p in range(len(is_prime)):
if is_prime[p]:
print(p, end=' ')
Test¶
is_prime = seive_of_eratosthenes(120)
print_primenumbers(is_prime)
Following are the prime numbers smaller than 121
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113