Maze Solver with A* Algorithm
Contents
Maze Solver with A* Algorithm¶

Fig. 26 Maze Solver A* Source: Wikipedia¶
A* Algorithm give always an optimal solution based on a bread-first-search and queues. It is an extension over the previous Lee’s Algorithms and Dijkstra’s Algorithms, and uses heuristics to guide its search.
A* Algorithm has the in the worst case the same time complexity as Dijkstra which is depending on the queue implementation, where \(|E|\) = number of edges and \(|V|\) number of nodes.
Fibonacci heap: \(O(|E| + |V| log |V|)\)
binary heap: \(O((|E| + |V|) log |V|)\)
unsorted array: \(O(|V|^2)\)
But A* is based on heuristics which helps to find a more optimal solution much quicker.

Fig. 27 A* Algorithms Demo Source: Wikipedia¶
Terminology¶
Node or State - All uniquely identifiable elements where it’s possible to stop
Transition - Moving between states
Source Node - Location to start the search
Destination Node - Location to be found
Search Space - A collection of nodes
Cost - Numerical value representing the cost for moving vom one node to another
Node Values¶
One important aspect of A* is the cost calculations. \(f(n) = g(n)+h(n)\). Every time a new node is created these values are calculated:
\(f(n)\) = Total cost of a node
\(g(n)\) = distance between current node and start node
\(h(n)\) = heuristic, estimated distance between current node and the end node
Fibonacci Heap¶
With Heap Collection method such as Binomial or Fibonacci Heap to collect the trees the algorithm can be more time efficient.
Fibonacci Head is a datastructure for priority queue operation. Fibonacci Heap maintains a pointer to minimum value (which is root of a tree). All tree roots are connected using circular doubly linked list, so all of them can be accessed using single ‘min’ pointer.
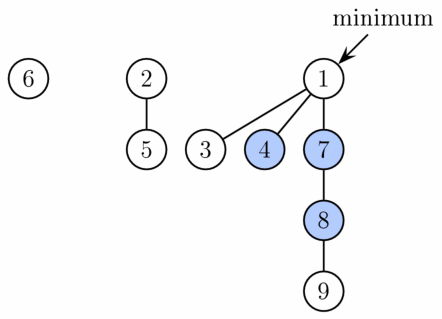
Fig. 28 Fibonacci Heap Source: Wikipedia¶
Solution¶
Flowchart of the solution
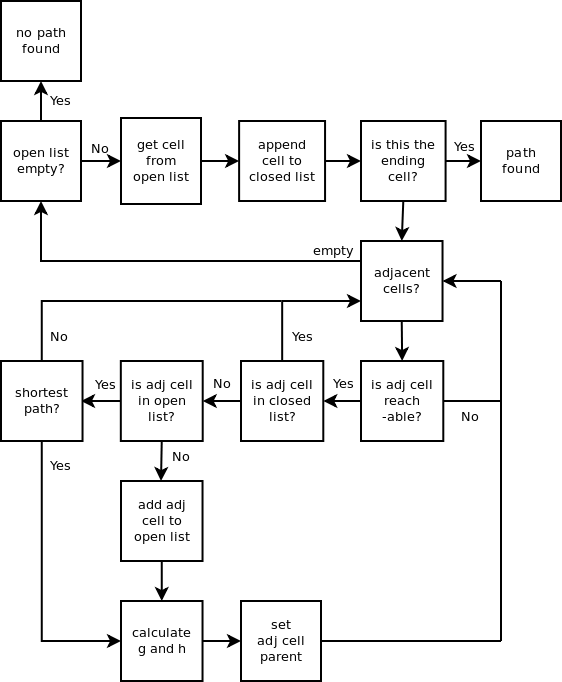
Fig. 29 A* Flowchart Source: Wikipedia¶
Pseudo code¶
// A* (star) Pathfinding
// Initialize both open and closed list
let the openList equal empty list of nodes
let the closedList equal empty list of nodes
// Add the start node
put the startNode on the openList (leave it's f at zero)
// Loop until you find the end
while the openList is not empty
// Get the current node
let the currentNode equal the node with the least f value
remove the currentNode from the openList
add the currentNode to the closedList
// Found the goal
if currentNode is the goal
Congrat! You've found the end! Backtrack to get path
// Generate children
let the children of the currentNode equal the adjacent nodes
for each child in the children
// Child is on the closedList
if child is in the closedList
continue to beginning of for loop
// Create the f, g, and h values
child.g = currentNode.g + distance between child and current
child.h = distance from child to end
child.f = child.g + child.h
// Child is already in openList
if child.position is in the openList's nodes positions
if the child.g is higher than the openList node's g
continue to beginning of for loop
// Add the child to the openList
add the child to the openList
Imports¶
import heapq
from IPython.display import clear_output
# generate maze from other notebook
# Run 008-maze-generation-kruskal notebook
%run 008-maze-generation-kruskal.ipynb
Algorithm¶
class Node:
def __init__(self, g: int = 0, h: int = 0, f: int = float("inf"), pos: list = []):
"""Representation of a cell, vertex or node
Args:
g (int): distance between node and source node
h (int): heuristic, estimated distance between node and destination
f (int): total cost of the node
pos (list): [y,x] position of the node in the maze
"""
self.g = g
self.h = h
self.f = f
self.pos = pos
def __eq__(self, other):
return (self.f == other.f)
def __ne__(self, other):
return not (self.f == other.f)
def __lt__(self, other):
return (self.f < other.f)
def __gt__(self, other):
return (self.f > other.f)
def __le__(self, other):
return (self.f <= other.f)
def __ge__(self, other):
return (self.f >= other.f)
def printNode(self, prefix: str = "", postfix: str = ""):
print("{}Node: [{},{}], g:{}, h:{} f:{}{}".format(prefix, self.pos[0], self.pos[1], self.g, self.h, self.f, postfix))
def aStar(maze, src: list, dest: list):
"""Function to find the shortest path between source cell and destination cell with help of the A* algorithm
Args:
maze (list): 2 dimensional maze matrix
src (list): y-x coordinates of source cell
dest (list): y-x coordinates of destination cell
Returns:
list: [distance of the solution, list of the maze solution path]
"""
# These arrays show the 4 possible movement from a cell
_rowNum = [-1, 0, 0, 1]
_colNum = [0, -1, 1, 0]
# store infinity
_infinity = float("inf")
# Checking if source and destination cell have value 1
if maze[src[0]][src[1]]!=1 or maze[dest[0]][dest[1]]!=1:
return None
# get maze size
_maze_rows = len(maze)
_maze_cols = len(maze[0])
# list of visited cells
_visited = [[False for i in range(_maze_cols)]
for j in range(_maze_rows)]
# list of distances fill with infinity
_f = [[_infinity for i in range(_maze_cols)]
for j in range(_maze_rows)]
# Create a queue
_unvisited = []
# create source node and mark as visited
_visited[src[0]][src[1]] = True
# manhatten distance to dst
_h = abs(dest[0] - src[0]) + abs(dest[1] - src[1])
# zero distance to source
_g = 0
# zero cost
_f[src[0]][src[1]] = 0
_node = Node(_g, _h, _f[src[0]][src[1]], src)
# enqueue src node
heapq.heappush(_unvisited, _node)
#_node.printNode("Push ")
# Perform A* starting from source cell
while _unvisited:
# shortest unexplored path
_cur_node = heapq.heappop(_unvisited)
#_cur_node.printNode("Pop ")
# add node to visited cells
_visited[_cur_node.pos[0]][_cur_node.pos[1]] = True
# If we have reached the destination cell, return the final distance
# return f distances in order to backtrack
if _cur_node.pos[0] == dest[0] and _cur_node.pos[1] == dest[1]:
return _f
# Extend path to all adjacent cells
for i in range(4):
_adj_node_pos = (_cur_node.pos[0] + _rowNum[i], _cur_node.pos[1] + _colNum[i])
# if not visited yet and within maze and a cell (1))
if (not _visited[_adj_node_pos[0]][_adj_node_pos[1]] and
((_adj_node_pos[0] >= 0) and (_adj_node_pos[0] < _maze_rows) and (_adj_node_pos[1] >= 0) and (_adj_node_pos[1] < _maze_cols)) and
(maze[_adj_node_pos[0]][_adj_node_pos[1]] == 1)):
# calculate f, g and h values
# calculate manhattan distance from cur_node to adj_node. Always one because it is a maze
_d = abs(_cur_node.pos[0] - _adj_node_pos[0]) + abs(_cur_node.pos[1] - _adj_node_pos[1])
# new distance
_g = _cur_node.g + _d
# manhattan distance from adj_node to dest
_h = abs(dest[0] - _adj_node_pos[0]) + abs(dest[1] - _adj_node_pos[1])
_f[_adj_node_pos[0]][_adj_node_pos[1]] = _g+_h
_adj_node = Node(_g, _h, _f[_adj_node_pos[0]][_adj_node_pos[1]], _adj_node_pos)
# see if node pos already existing in list (this should be improved)
_in_list = False
for node in _unvisited:
if node.pos == _adj_node.pos:
if _adj_node.g > node.g:
_in_list = True
if not _in_list:
heapq.heappush(_unvisited, _adj_node)
#_adj_node.printNode("Push ")
# Return none if destination cannot be reached
return None
def getSolution(src: list, dst: list, f: list):
"""Get shortest solution path
Args:
src (list): y,x coordinates of the startpoint
f (list): array of costs for each cell to arrive at the destination
Returns:
list: optimum solution path
"""
_solution_path = []
# These arrays show the 4 possible movement from a cell
_rowNum = [-1, 0, 0, 1]
_colNum = [0, -1, 1, 0]
# get maze size
_maze_rows = len(f)
_maze_cols = len(f[0])
_maze_size = _maze_cols*_maze_rows
_cur_pos = dst
_prev_pos = dst
# get maximum distance
_arrived = False
j = 0
while(not _arrived and j <= _maze_size):
_cost = float("inf")
# for all 4 adjacent cells select the one with the smallest cost
for i in range(len(_rowNum)):
_next_pos = [_cur_pos[0] + _rowNum[i], _cur_pos[1] + _colNum[i]]
# check in on the board
if (_next_pos[0] >= 0) and (_next_pos[0] < _maze_rows) and (_next_pos[1] >= 0) and (_next_pos[1] < _maze_cols):
# Check if not the previous cell
if not (_prev_pos == _next_pos):
if f[_next_pos[0]][_next_pos[1]] < _cost:
_temp_pos = _next_pos
_cost = f[_next_pos[0]][_next_pos[1]]
if _cost != float("inf"):
_solution_path.append(_temp_pos)
_prev_pos = _cur_pos
_cur_pos = _temp_pos
if _cur_pos == src:
return _solution_path
j += 1
def drawSolution(maze: list, src: list, dst: list, solutionpath: list):
"""draw the start- and endpoint as well as the solution
0 = wall
1 = cell
2 = path
3 = start- endpoint
Args:
maze (list): 2 dimensional array of the maze
src (list): y,x coordinates of the startpoint
dst (list): y,x coordinates of the endpoint
solutionpath (list): array of points of the solution
Returns:
list: 2d array of the maze including solution
"""
maze_tmp = maze.copy()
# draw solution
for point in solutionpath:
maze_tmp[point[0]][point[1]] = 2
# draw start and endpoint
maze_tmp[src[0]][src[1]] = 3
maze_tmp[dst[0]][dst[1]] = 3
return maze_tmp
def findEmptyCell(maze: list, corner: int):
"""find empty cell in cell starting at a corner
Args:
maze (list): maze to search through
corner (int): where to start (0=bottomleft, 1=topleft, 2=topright, 3=bottomright)
Returns:
list: row,col coordinates of the first empty cell
"""
maze_rows = len(maze)
maze_cols = len(maze[0])
if corner == 0:
range_rows = range(0, maze_rows-1, 1)
range_cols = range(0, maze_cols-1, 1)
elif corner == 1:
range_rows = range(0, maze_rows-1, 1)
range_cols = range(maze_cols-1, 0, -1)
elif corner == 2:
range_rows = range(maze_rows-1, 0, -1)
range_cols = range(maze_cols-1, 0, -1)
else:
range_rows = range(maze_rows-1, 0, -1)
range_cols = range(0, maze_cols-1, 1)
# find empty cell
for row in range_rows:
for col in range_cols:
if maze[row][col] == 1: # valid cell found
return [row, col]
Test¶
no_solution = True
while no_solution:
# generate maze with function from 008 notebook
size = {'x': 80,'y': 40}
maze = generateMaze(size['x'], size['y'])
maze = createBorder(maze)
# get maze size
maze_rows = len(maze)
maze_cols = len(maze[0])
# find empty cell in topleft corner
src = findEmptyCell(maze, 0)
# find empty cell in bottomright corner
dst = findEmptyCell(maze, 2)
print("Maze Size : {}x{}".format(maze_cols, maze_rows))
print("Source Cell is : {}".format(src))
print("Destination Cell is : {}".format(dst))
# execute A* algorithm
f = aStar(maze, src, dst)
# draw points and solution
if f:
no_solution = False
path = getSolution(src, dst, f)
print("Length of the Shortest Path is", len(path))
maze_solved = drawSolution(maze, src, dst, path)
else:
#no_solution = False##
print("No solution exists")
clear_output(wait=True)
Maze Size : 81x41
Source Cell is : [1, 10]
Destination Cell is : [39, 76]
Length of the Shortest Path is 144
output_notebook()
plot = figure(x_range=(0, 1), y_range=(0, 1),
plot_height=maze_rows*10, plot_width=maze_cols*10)
plot.axis.visible = False
plot.outline_line_color = '#ffffff'
plot.image([maze_solved], x=0, y=0, dw=1, dh=1, palette=['#228b22', '#ffffff', '#add8e6', '#ff7f7f'])
show(plot)