Sorting Algorithms
Contents
Sorting Algorithms¶

Fig. 35 Overview of Sorting algorithms Source: https://www.toptal.com/developers/sorting-algorithms¶
The counterpart of searching algorithms such as Binary Search are sorting algorithms. They are necessary to optimize data searching. It is also used to represent data in more readable format. Depending on the different algorithms and the current problem different algorithms can be best.
Interesting links
Theory¶
Classification of algorithms¶
Time-Space Complexity aka Big-O Notation for the best and the worst case scenario
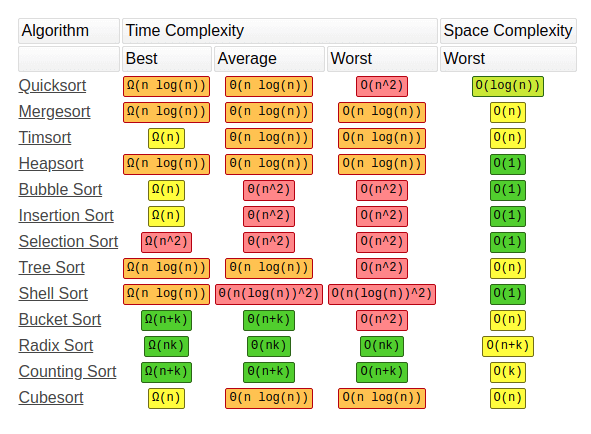
Fig. 36 Overview of Sorting algorithms complexity Source: https://totheinnovation.com/sorting-algorithms/¶
Number of swaps
Memory usage
Recursive vs Unrecursive
In-place vs Not-in-place
Sorting algorithms can either may required extra space for temporary storage. Algorithms not require extra space is called in-place sorting and algorithms require extra space is calles not-in-place sorting.
Stable vs Unstable
If the sorting elements does not change the sequence of similar elements it if called stable sorting. If the similar elements after sorting have changed order it is called unstable sorting.
Adaptability
Types¶
Worst to best \(O(n!)\) \(O(2^n)\) \(O(n^2)\) \(O(n(log(n))^2)\) \(O(n log(n))\) \(O(n)\) \(O(k)\) \(O(n+k)\) \(O(nk)\) \(O(log(n))\) \(O(1)\)
Algorithm |
Time Compl. (Best) |
Time Compl. (Average) |
Time Compl. (Worst) |
Space Compl. (Worst) |
Type |
|---|---|---|---|---|---|
\(O(n)\) |
\(O(n^2)\) |
\(O(n^2)\) |
\(O(1)\) |
Adaptive, Stable, In-place, Online |
|
\(O(n^2)\) |
\(O(n^2)\) |
\(O(n^2)\) |
\(O(1)\) |
In-place, Stable |
|
\(O(n)\) |
\(O(n^2)\) |
\(O(n^2)\) |
\(O(1)\) |
Stable |
|
\(O(n log(n))\) |
\(O(n(log(n))^2)\) |
\(O(n(log(n))^2)\) |
\(O(1)\) |
In-place, Not-Stable, Adaptive |
|
\(O(n log(n))\) |
\(O(n log(n))\) |
\(O(n log(n))\) |
\(O(n)\) |
Divide and Conquer, Stable, Not-in-place |
|
\(O(n log(n))\) |
\(O(n log(n))\) |
\(O(n log(n))\) |
\(O(1)\) |
Not Stable, In-Place, |
|
\(O(n log(n))\) |
\(O(n log(n))\) |
\(O(n^2)\) |
\(O(log(n))\) |
Divide and Conquer, In-place, Not-stable |
|
\(O(n+k)\) |
\(O(n+k)\) |
\(O(n^2)\) |
\(O(n)\) |
Not-in-place, Stable |
|
\(O(nk)\) |
\(O(nk)\) |
\(O(nk)\) |
\(O(n+k)\) |
Adaptive, Various versions |
|
\(O(n+k)\) |
\(O(n+k)\) |
\(O(n+k)\) |
\(O(k)\) |
Not-in-place, Stable |
Implementation¶
Imports¶
import random
import time
import pandas as pd
import bokeh.io as bio
import bokeh.plotting as bp
import bokeh.layouts as bl
Helpers¶
def createSortedList(size: int = 10, ascending: bool = True):
"""Create a sorted list 0 -> size-1
Args:
size (int, optional): size of list. Defaults to 10.
ascending (bool, optional): sorted ascending or descending. Defaults to True.
Returns:
list: list of values
"""
_lst = list(range(1, size+1))
if not ascending:
_lst.sort(reverse=True)
return _lst
def createRandomList(size: int = 10):
"""Create a unsorted list with all values 0 -> size-1
Args:
size (int, optional): size of list. Defaults to 10.
Returns:
list: list of values
"""
_lst = createSortedList(size)
random.shuffle(_lst)
return _lst
def createNearlySortedList(size: int = 10, unsorted: float = 0.05):
"""Create a nearly sorted list with all values 0 -> size-1
min 1 max (unsorted*100)% of values are unsorted
Args:
size (int, optional): size of list. Defaults to 10.
unsorted(float, optional): value between 0 and 1 % of unsorted values. Default to 0.05.
Returns:
list: list of values
"""
_lst = createSortedList(size)
_nbr_of_unsorted = int(size*unsorted)
if _nbr_of_unsorted < 1:
_nbr_of_unsorted = 1
for i in range(_nbr_of_unsorted):
_idx_1 = random.randint(0, len(_lst)-1)
_idx_2 = random.randint(0, len(_lst)-1)
# swap elements
_temp = _lst[_idx_1]
_lst[_idx_1] = _lst[_idx_2]
_lst[_idx_2] = _temp
return _lst
def fewUniqueList(size: int = 10, nbr_of_bin: int = 3):
"""Create list of only a few unique values
Args:
size (int, optional): size of list. Defaults to 10.
nbr_of_bin (int, optional): number of unique values. Defaults to 3.
Returns:
list: list of values
"""
_lst = []
# select values and add appropriate number of times
for i in range(nbr_of_bin):
_value = random.randint(0, size)
for j in range(int(size/nbr_of_bin)):
_lst.append(_value)
# fill up if binsize not equal
while(len(_lst) < size):
_lst.append(_lst[-1])
# shuffle list
random.shuffle(_lst)
return _lst
def generateColorList(colors_idx: list):
"""Generate color list from list with values between 0 and 2
Args:
colors_idx (list): list of color values between 0 and 2
Returns:
list: list of preselected bokeh colors
"""
# Color options
colors = ["lightslategray", "dodgerblue", "hotpink"]
color_list = []
for elem in colors_idx:
color_list.append(colors[elem])
return color_list
def generateColors(size: int = 20):
"""Generate 0 filled color dataframe
Args:
size (int, optional): size of dataframes. Defaults to 20.
Returns:
object: dataframe with zero filled lists
"""
# Create dataframe
df_color = pd.DataFrame()
df_color["Sorted ascending"] = [0] * size
df_color["Sorted descending"] = [0] * size
df_color["Random"] = [0] * size
df_color["Nearly sorted"] = [0] * size
df_color["Few uniques"] = [0] * size
return df_color
def generateDf(size: int = 20):
"""Generate data list with different sorting styles
Args:
size (int, optional): size of dataframes. Defaults to 20.
Returns:
object: dataframe of various lists
"""
# Create dataframe
df_data = pd.DataFrame()
df_data["Sorted ascending"] = createSortedList(size)
df_data["Sorted descending"] = createSortedList(size, False)
df_data["Random"] = createRandomList(size)
df_data["Nearly sorted"] = createNearlySortedList(size)
df_data["Few uniques"] = fewUniqueList(size, int(size/2))
return df_data
def plotBokehs(df_data: object, df_colors_idx: object, size: int = 170):
"""Plot all columns in dataframe with custom colors
Args:
df_data (dataframe): df with columns to plot
df_colors_idx (dataframe): corresponding color between 0 and 2 for the df_data values
size (int, optional): size in px of one subfigure. Defaults to 200.
Returns:
list: list of figure objects
"""
bio.output_notebook()
figs = []
for column in df_data.columns:
# get color list
colors = generateColorList(df_colors_idx[column])
# Just number list 0 to n for y axis
y = list(range(0, len(df_data[column])))
# create figure
fig = bp.figure(title=column, plot_width=size, plot_height=size, toolbar_location=None)
fig.hbar(y=y, right=df_data[column], left=0, height=1, color=colors)
fig.axis.visible = False
figs.append(fig)
handle = bio.show(bl.row(figs), notebook_handle=True)
return figs, handle
def plotBokeh(data: object, colors_idx: object, name: str = "", size: int = 170):
"""Plot a list dataframe with custom colors
Args:
data (list): list of data to plot
colors_idx (list): corresponding color list between 0 and 2 for the data values
name (str): plot title
size (int, optional): size in px of one subfigure. Defaults to 200.
Returns:
list: list of figure objects
"""
bio.output_notebook()
# get color list
colors = generateColorList(colors_idx)
# Just number list 0 to n for y axis
y = list(range(0, len(data)))
# create figure
fig = bp.figure(title=name, plot_width=size, plot_height=size, toolbar_location=None)
fig.hbar(y=y, right=data, left=0, height=1, color=colors)
fig.axis.visible = False
handle = bio.show(bl.row(figs), notebook_handle=True)
return fig, handle
def updateBokeh(color, idx, value, fig: object, display: bool, sleeptime=0.1):
if display:
color[idx] = value
time.sleep(sleeptime)
# update graph
# fig
return color
Test Helpers¶
size = 20
# Generate Data
df_data = generateDf(size)
df_color = generateColors(size)
# Change some bar colors
df_color.at[0, "Sorted ascending"] = 1
df_color.at[0, "Sorted descending"] = 1
df_color.at[0, "Random"] = 1
df_color.at[0, "Nearly sorted"] = 1
df_color.at[0, "Few uniques"] = 1
df_color.at[1, "Sorted ascending"] = 2
df_color.at[1, "Sorted descending"] = 2
df_color.at[1, "Random"] = 2
df_color.at[1, "Nearly sorted"] = 2
df_color.at[1, "Few uniques"] = 2
# Plot
plotBokehs(df_data, df_color);
Insert Sort¶
Insert Sort is a simple sorting algorithm, is becomes less efficient the larger the dataset is. However advantages are: simple implementation, efficient for small datasets, adaptive, stable, in-place, online.
Time Compl. (Best) |
Time Compl. (Average) |
Time Compl. (Worst) |
Space Compl. (Worst) |
Type |
|---|---|---|---|---|
\(O(n)\) |
\(O(n^2)\) |
\(O(n^2)\) |
\(O(1)\) |
Adaptive, Stable, In-place, Online |
Algorithms
Iterate over the unsorted input elements starting with the left most element
Compare the current element with the largest value available in the sorted array. Sorted array is left of the element
If the current element is greater, then it leaves the element in its place and moves on to the next element, else it finds its correct position in the sorted array and moves it to that position in the array.
This is achieved by shifting all the elements towards the right, which are larger than the current element, in the sorted array to one position ahead.
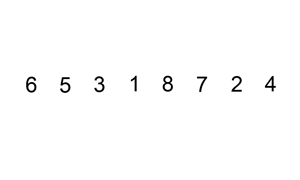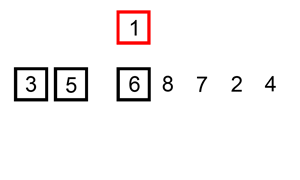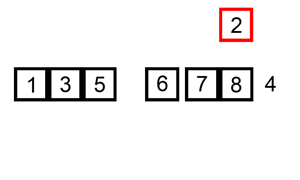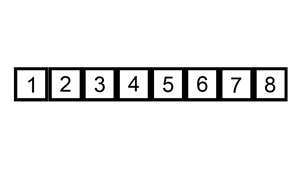
Fig. 37 Insert sort Source: Wikipedia¶
Pseudocode
i ← 1
while i < length(A)
j ← i
while j > 0 and A[j-1] > A[j]
swap A[j] and A[j-1]
j ← j - 1
end while
i ← i + 1
end while
def insertionSort(lst: list, fig: object = None, display: bool = True):
"""insertion Sort of list including updating figure
Args:
lst (list): unsorted list
fig (object, optional): figure to update. Defaults to None.
display (bool, optional): update graph also slows down operation. Defaults to True.
Returns:
lst: sorted list
"""
# create color idx list init with 0 (only used for display)
color = [0] * len(lst)
# llop through list starting at 1 (0 cannot be moved)
for idx in range(1, len(lst)):
color = updateBokeh(color, idx, 1, fig, display)
elem = lst[idx]
# Move elements of lst[0..i-1], that are greater than key, to one position ahead of their current position
prev_idx = idx-1
while prev_idx >= 0 and elem < lst[prev_idx]:
color = updateBokeh(color, prev_idx, 2, fig, display)
lst[prev_idx+1] = lst[prev_idx]
color = updateBokeh(color, prev_idx, 0, fig, display)
prev_idx -= 1
lst[prev_idx+1] = elem
color = updateBokeh(color, idx, 0, fig, display)
return lst
Test¶
size = 20
# Generate Data
df_data = generateDf(size)
df_color = generateColors(size)
# display original list
figs, handle = plotBokehs(df_data, df_color)
i = 0
for column in df_data.columns:
df_data[column] = insertionSort(df_data[column], figs[i], True)
i += 1
# display sorted list
plotBokehs(df_data, df_color);
Selection Sort¶
Time Compl. (Best) |
Time Compl. (Average) |
Time Compl. (Worst) |
Space Compl. (Worst) |
Type |
|---|---|---|---|---|
\(O(n^2)\) |
\(O(n^2)\) |
\(O(n^2)\) |
\(O(1)\) |
In-place, Stable |
Bubble Sort¶
Time Compl. (Best) |
Time Compl. (Average) |
Time Compl. (Worst) |
Space Compl. (Worst) |
Type |
|---|---|---|---|---|
\(O(n)\) |
\(O(n^2)\) |
\(O(n^2)\) |
\(O(1)\) |
Stable |
Shell Sort¶
Time Compl. (Best) |
Time Compl. (Average) |
Time Compl. (Worst) |
Space Compl. (Worst) |
Type |
|---|---|---|---|---|
\(O(n log(n))\) |
\(O(n(log(n))^2)\) |
\(O(n(log(n))^2)\) |
\(O(1)\) |
In-place, Not-Stable, Adaptive |
Merge Sort¶
Time Compl. (Best) |
Time Compl. (Average) |
Time Compl. (Worst) |
Space Compl. (Worst) |
Type |
|---|---|---|---|---|
\(O(n log(n))\) |
\(O(n log(n))\) |
\(O(n log(n))\) |
\(O(n)\) |
Divide and Conquer, Stable, Not-in-place |
Heap Sort¶
Time Compl. (Best) |
Time Compl. (Average) |
Time Compl. (Worst) |
Space Compl. (Worst) |
Type |
|---|---|---|---|---|
\(O(n log(n))\) |
\(O(n log(n))\) |
\(O(n log(n))\) |
\(O(1)\) |
Not Stable, In-Place, |
Quick Sort¶
Time Compl. (Best) |
Time Compl. (Average) |
Time Compl. (Worst) |
Space Compl. (Worst) |
Type |
|---|---|---|---|---|
\(O(n log(n))\) |
\(O(n log(n))\) |
\(O(n^2)\) |
\(O(log(n))\) |
Divide and Conquer, In-place, Not-stable |
Bucket Sort¶
Time Compl. (Best) |
Time Compl. (Average) |
Time Compl. (Worst) |
Space Compl. (Worst) |
Type |
|---|---|---|---|---|
\(O(n+k)\) |
\(O(n+k)\) |
\(O(n^2)\) |
\(O(n)\) |
Not-in-place, Stable |
Radix Sort¶
Time Compl. (Best) |
Time Compl. (Average) |
Time Compl. (Worst) |
Space Compl. (Worst) |
Type |
|---|---|---|---|---|
\(O(nk)\) |
\(O(nk)\) |
\(O(nk)\) |
\(O(n+k)\) |
Adaptive, Various versions |
Counting Sort¶
Time Compl. (Best) |
Time Compl. (Average) |
Time Compl. (Worst) |
Space Compl. (Worst) |
Type |
|---|---|---|---|---|
\(O(n+k)\) |
\(O(n+k)\) |
\(O(n+k)\) |
\(O(k)\) |
Not-in-place, Stable |