Maze Solver with Dijkstra’s Algorithm
Contents
Maze Solver with Dijkstra’s Algorithm¶

Fig. 21 Dijkstra Maze Solution¶
Djikstra’s Algorithm give always an optimal solution based on a bread-first-search and queues. It is an improvement over the previous Lee’s Algorithms, since the distance (costs) to the starting point is kept updated in a queue.
Dijkstra’s Algorithm has different time complexities depending in the queue implementation, where
Fibonacci heap:
binary heap:
unsorted array:

Fig. 22 Maze Solver Dijkstra Source: Wikipedia¶
The graph is has 2 elements: vertices and edges.
Fibonacci Heap¶
With Heap Collection method such as Binomial or Fibonacci Heap to collect the trees the algorithm can be more time efficient.
Fibonacci Head is a datastructure for priority queue operation. Fibonacci Heap maintains a pointer to minimum value (which is root of a tree). All tree roots are connected using circular doubly linked list, so all of them can be accessed using single ‘min’ pointer.
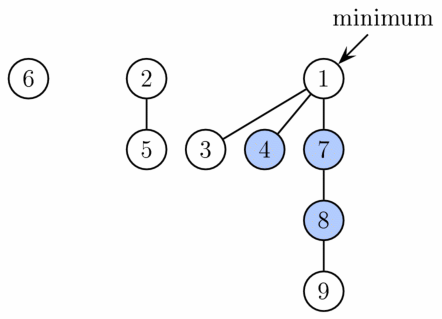
Fig. 23 Fibonacci Heap Source: Wikipedia¶
Solution¶
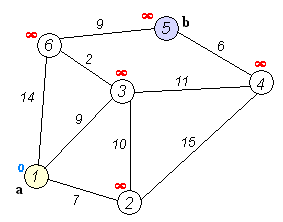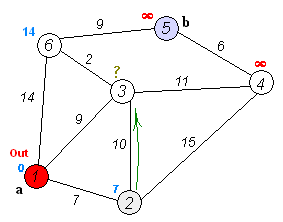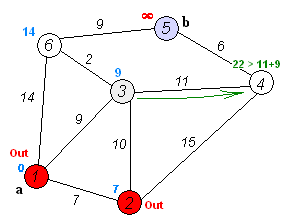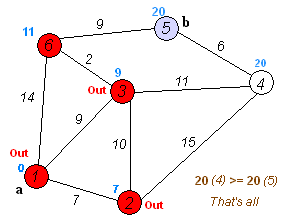
Fig. 24 Dijkstra Solver Step by Step Source: Wikipedia¶
Start with a weighted graph
Fig. 25 Dijkstra weighted graph, based on Algotree.org¶
Choose the start vertex and assign infinity path values to all other devices
Got to each adjacent vertex and update its path length
If the path length is calculated is longer, don’t update it otherwise update it
After each iteration pick the unvisited vertex with the least path length
Repeat until all vertices have been visited
Pseudo code¶
function dijkstra(G, S)
for each vertex V in G
distance[V] <- infinite
previous[V] <- NULL
If V != S, add V to Priority Queue Q
distance[S] <- 0
while Q IS NOT EMPTY
U <- Extract MIN from Q
for each unvisited neighbour V of U
tempDistance <- distance[U] + edge_weight(U, V)
if tempDistance < distance[V]
distance[V] <- tempDistance
previous[V] <- U
return distance[], previous[]
Additional Information¶
Washington University paper CSE326: Data Structures Dijkstra Algorithm (James Fogarty, 2007).
For a maze where the next possible vertex are up, down, left and right with the same distance/costs the dijkstra ha no real advantage over lee.
Imports¶
import heapq
from IPython.display import clear_output
# generate maze from other notebook
# Run 008-maze-generation-kruskal notebook
%run 008-maze-generation-kruskal.ipynb
Algorithm¶
def dijkstra(maze, src: list, dest: list):
"""Function to find the shortest path between source cell and destination cell with help of the dijkstra algorithm
Args:
maze (list): 2 dimensional maze matrix
src (list): y-x coordinates of source cell
dest (list): y-x coordinates of destination cell
Returns:
list: [distance of the solution, list of the maze solution path,]
"""
# These arrays show the 4 possible movement from a cell
rowNum = [-1, 0, 0, 1]
colNum = [0, -1, 1, 0]
# Solution path, list of [y,x] coordinates
solution = []
# Checking if source and destination cell have value 1
if maze[src[0]][src[1]]!=1 or maze[dest[0]][dest[1]]!=1:
return None
# get maze size
maze_rows = len(maze)
maze_cols = len(maze[0])
# list of visited cells
visited = [[False for i in range(maze_cols)]
for j in range(maze_rows)]
# Mark the source cell as visited
visited[src[0]][src[1]] = True
# Create a queue
queue = []
# node [distance, [coordinates]]
# Distance of source cell is 0
node = [0,src]
# enqueue src node
heapq.heappush(solution, node)
heapq.heappush(queue, node)
# Perform dijkstra starting from source cell
while queue:
# shortest unexplored path
dist, vertex = heapq.heappop(queue)
# If we have reached the destination cell, return the final distance
if vertex[0] == dest[0] and vertex[1] == dest[1]:
return solution
# Otherwise enqueue its adjacent cells (extend path)
for i in range(4):
row = vertex[0] + rowNum[i]
col = vertex[1] + colNum[i]
# Enqueue valid adjacent cell that is not visited
if (((row >= 0) and (row < maze_rows) and (col >= 0) and (col < maze_cols)) and
maze[row][col] == 1 and
not visited[row][col]):
visited[row][col] = True
adjcell = [dist+1, [row, col]] # add distance to neighbor cell (+1)
heapq.heappush(solution, adjcell)
heapq.heappush(queue, adjcell)
# Return none if destination cannot be reached
return None
def checkAdjacent(point_1: list, point_2: list):
"""Check of
Args:
point_1 (list): y,x coordinates of first point
point_2 (list): y,x coordinates of second point
Returns:
bool: true if cell is adjacent
"""
# These arrays show the 4 possible movement from a cell
_rowNum = [-1, 0, 0, 1]
_colNum = [0, -1, 1, 0]
_adjacent = False
for i in range(len(_rowNum)):
if point_1[0] == point_2[0]+_rowNum[i] and point_1[1] == point_2[1]+_colNum[i]:
_adjacent = True
return _adjacent
def getSolution(src: list, dst: list, solution: list):
"""Get shortest solution path
Args:
src (list): y,x coordinates of the startpoint
solution (list): array of distance to the src-point and points of the solution
Returns:
list: optimum solution path
"""
_solution_path = []
# get maximum distance
_distance = None
_prev_cell = None
for i in range(len(solution)-1, 0, -1):
if not _distance and not _prev_cell:
if solution[i][1] == dst: # found destination point start pathsearch
_distance = solution[i][0] - 1
_prev_cell = solution[i][1]
else:
if _distance == solution[i][0] and checkAdjacent(solution[i][1], _prev_cell): # if correct distance and if adjacent cell
_solution_path.append(solution[i][1])
_distance -= 1
_prev_cell = solution[i][1]
return _solution_path
def drawSolution(maze: list, src: list, dst: list, solutionpath: list):
"""draw the start- and endpoint as well as the solution
0 = wall
1 = cell
2 = path
3 = start- endpoint
Args:
maze (list): 2 dimensional array of the maze
src (list): y,x coordinates of the startpoint
dst (list): y,x coordinates of the endpoint
solutionpath (list): array of points of the solution
Returns:
list: 2d array of the maze including solution
"""
maze_tmp = maze.copy()
# draw solution
for point in solutionpath:
maze_tmp[point[0]][point[1]] = 2
# draw start and endpoint
maze_tmp[src[0]][src[1]] = 3
maze_tmp[dst[0]][dst[1]] = 3
return maze_tmp
def findEmptyCell(maze: list, corner: int):
"""find empty cell in cell starting at a corner
Args:
maze (list): maze to search through
corner (int): where to start (0=bottomleft, 1=topleft, 2=topright, 3=bottomright)
Returns:
list: row,col coordinates of the first empty cell
"""
maze_rows = len(maze)
maze_cols = len(maze[0])
if corner == 0:
range_rows = range(0, maze_rows-1, 1)
range_cols = range(0, maze_cols-1, 1)
elif corner == 1:
range_rows = range(0, maze_rows-1, 1)
range_cols = range(maze_cols-1, 0, -1)
elif corner == 2:
range_rows = range(maze_rows-1, 0, -1)
range_cols = range(maze_cols-1, 0, -1)
else:
range_rows = range(maze_rows-1, 0, -1)
range_cols = range(0, maze_cols-1, 1)
# find empty cell
for row in range_rows:
for col in range_cols:
if maze[row][col] == 1: # valid cell found
return [row, col]
Test¶
no_solution = True
while no_solution:
# generate maze with function from 008 notebook
size = {'x': 80, 'y': 40}
maze = generateMaze(size['x'], size['y'])
maze = createBorder(maze)
# get maze size
maze_rows = len(maze)
maze_cols = len(maze[0])
# find empty cell in topleft corner
src = findEmptyCell(maze, 0)
# find empty cell in bottomright corner
dst = findEmptyCell(maze, 2)
print("Maze Size : {}x{}".format(maze_cols, maze_rows))
print("Source Cell is : {}".format(src))
print("Destination Cell is : {}".format(dst))
# execute dijkstra's algorithms
solution = dijkstra(maze, src, dst)
# draw points and solution
if solution:
no_solution = False
path = getSolution(src, dst, solution)
print("Length of the Shortest Path is", solution[-1][0])
maze_solved = drawSolution(maze, src, dst, path)
else:
#no_solution = False##
print("No solution exists")
clear_output(wait=True)
Maze Size : 81x41
Source Cell is : [1, 6]
Destination Cell is : [39, 78]
Length of the Shortest Path is 243
output_notebook()
plot = figure(x_range=(0, 1), y_range=(0, 1),
plot_height=maze_rows*10, plot_width=maze_cols*10)
plot.axis.visible = False
plot.outline_line_color = '#ffffff'
plot.image([maze_solved], x=0, y=0, dw=1, dh=1, palette=['#228b22', '#ffffff', '#add8e6', '#ff7f7f'])
show(plot)