Big O Notation

The Big O notation indicates how fast an algorithms is. It is the worst case evaluation of the given algorithms. In short, how many iterations are needed in the worst case. A list of algorithms with theirs Big O notation can be found at https://big-o.io.

O(n)
 ^ ^
 | +-- Number of operations
 +---- Big O

Figure 1: BigO Runtimes Source: https://big-o.io

Some common runtimes

• \(O(log\;n)\) - also known as log time
  • Binary Search
• \(O(n)\) also known as linear time
  • Simple search
• \(O(n*log\;n)\) - fast sorting algorithms
• quicksort
• \(O(n^2)\) - slow sorting algorihtms
  • selection sort
• \(O(n!)\) - very slow algorithms
  • traveling salesperson

Figure 2: BigO Complexity Source: https://www.bigocheatsheet.com/

Figure 3: BigO Comparison Source: https://medium.com/@cparusso/what-the-hell-is-big-o-notation-9b90d9f9cd14

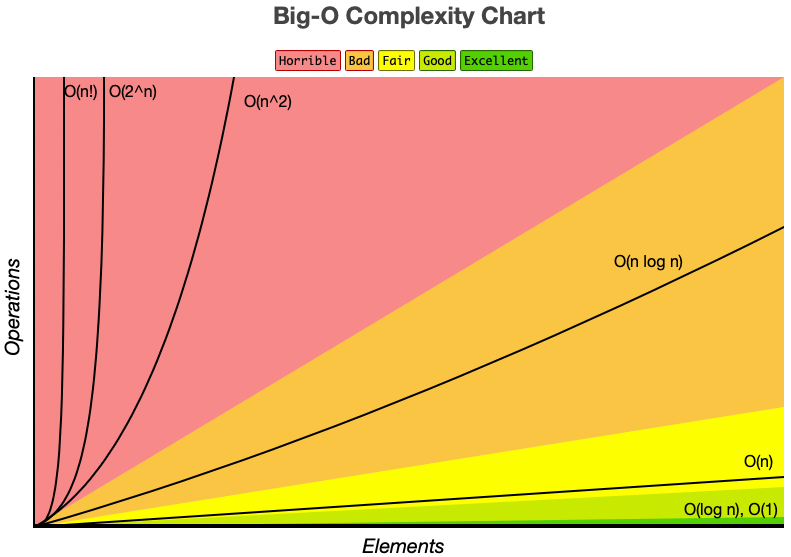
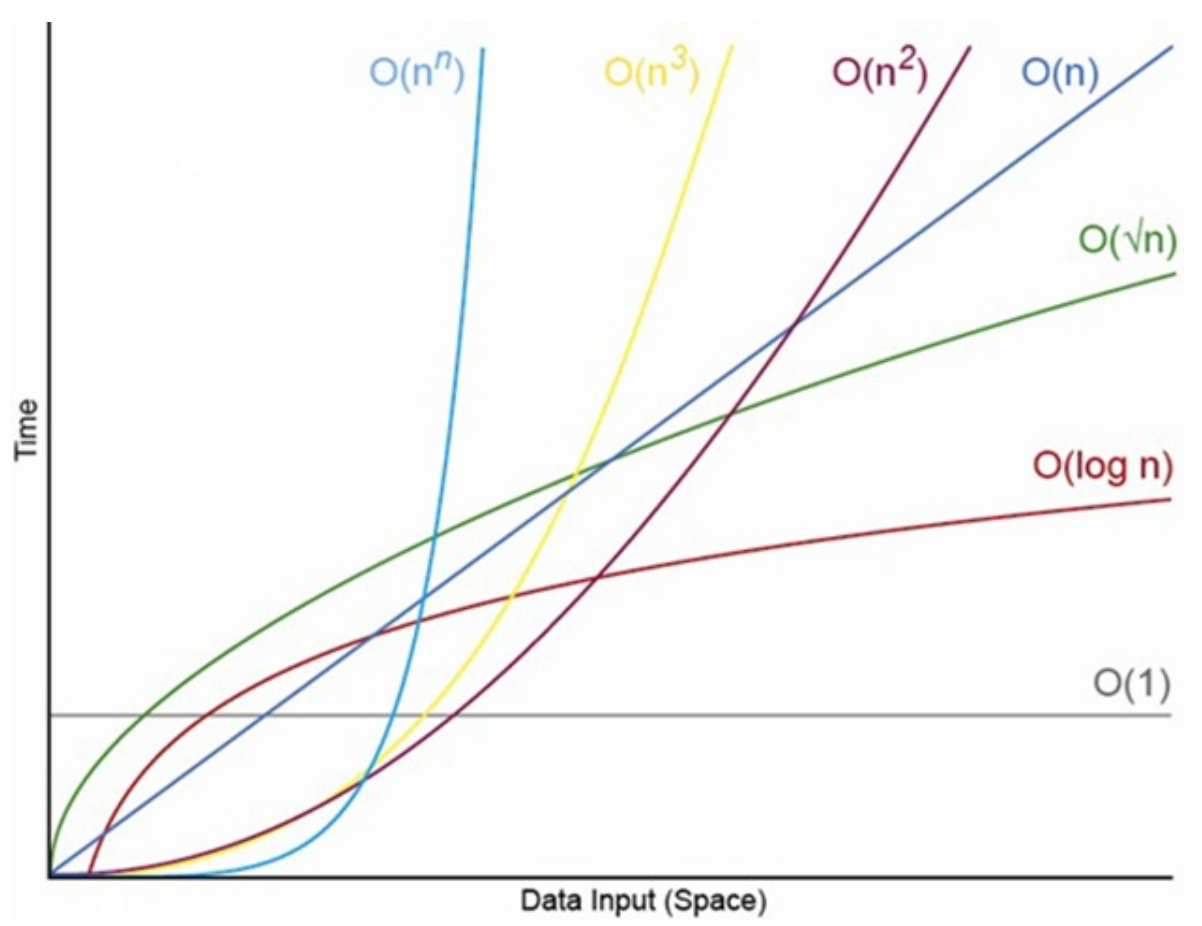
Ranking Worst to Best

• \(O(n!)\)
• \(O(2^n)\)
• \(O(n^2)\)
• \(O(n*(log\;n)^2)\)
• \(O(n*log\;n)\)
• \(O(n)\)
• \(O(k)\)
• \(O(n + k)\)
• \(O(nk)\)
• \(O(log\;n)\)
• \(O(1)\)