Maze Solver with Lee's Algorithm¶
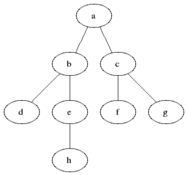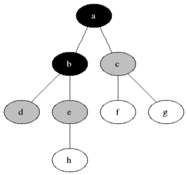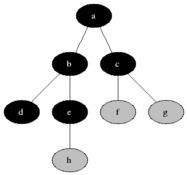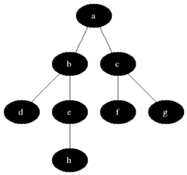
Lee's Algorithm give always an optimal solution based on a bread-first-search and queues. It requires considerable amount of memory and is slow.

Solution¶
Create an empty queue to store the coordinates of the matrix and initialize it with the source cell having a distance of 0 from the source, marking it as visited.
Starting from the source cell, call the BFS procedure.
Initialize a boolean array of the same size as input matrix and all values set to false. This is used to store the visited status of a coordinate.
Run a loop till the queue is empty
Dequeue front cell from the queue
Return if the destination cell is reached
Otherwise, For each of the four adjacent cells of a current cell, if the cell value is 1 and they are un-visited, enqueue the cells and mark them as visited.
If all queue elements are processed and destination is not reached, return false.
Imports¶
from collections import deque
from IPython.display import clear_output
# generate maze from other notebook
# Run 008-maze-generation-kruskal notebook
%run 008-maze-generation-kruskal.ipynb
Algorithm¶
def bfsLee(maze, src: list, dest: list):
"""Function to find the shortest path between source cell and destination cell.
Args:
maze (list): 2 dimensional maze matrix
src (list): y-x coordinates of source cell
dest (list): y-x coordinates of destination cell
Returns:
list: [list of the maze solution path, distance of the solution]
"""
# These arrays show the 4 possible movement from a cell
rowNum = [-1, 0, 0, 1]
colNum = [0, -1, 1, 0]
# Solution path, list of [y,x] coordinates
solution = []
# Checking if source and destination cell have value 1
if maze[src[0]][src[1]]!=1 or maze[dest[0]][dest[1]]!=1:
return None, -1
# get maze size
maze_rows = len(maze)
maze_cols = len(maze[0])
# list of visited cells
visited = [[False for i in range(maze_cols)]
for j in range(maze_rows)]
# Mark the source cell as visited
visited[src[0]][src[1]] = True
# Create a queue for BFS
queue = deque()
# node [[coordinates], distance]
# Distance of source cell is 0
node = [src,0]
solution.append(node)
# enqueue src node
queue.append(node)
# distance
# Perform BFS starting from source cell
while queue:
cur = queue.popleft() # Dequeue the front cell
# If we have reached the destination cell, return the final distance
pt = cur[0]
if pt[0] == dest[0] and pt[1] == dest[1]:
return solution, cur[1]
# Otherwise enqueue its adjacent cells with value 1
for i in range(4):
row = pt[0] + rowNum[i]
col = pt[1] + colNum[i]
# Enqueue valid adjacent cell that is not visited
if (((row >= 0) and (row < maze_rows) and (col >= 0) and (col < maze_cols)) and
maze[row][col] == 1 and
not visited[row][col]):
visited[row][col] = True
adjcell = [[row,col], cur[1]+1]
solution.append(adjcell)
queue.append(adjcell)
# Return -1 if destination cannot be reached
return None, -1
def checkAdjacent(point_1: list, point_2: list):
"""Check of
Args:
point_1 (list): y,x coordinates of first point
point_2 (list): y,x coordinates of second point
Returns:
bool: true if cell is adjacent
"""
# These arrays show the 4 possible movement from a cell
_rowNum = [-1, 0, 0, 1]
_colNum = [0, -1, 1, 0]
_adjacent = False
for i in range(len(_rowNum)):
if point_1[0] == point_2[0]+_rowNum[i] and point_1[1] == point_2[1]+_colNum[i]:
_adjacent = True
return _adjacent
def getSolution(src: list, dst: list, solution: list):
"""Get shortest solution path
Args:
src (list): y,x coordinates of the startpoint
solution (list): array of points of the solution and their distance to the src-point
Returns:
list: optimum solution path
"""
_solution_path = []
# get maximum distance
_distance = None
_prev_cell = None
for i in range(len(solution)-1, 0, -1):
if not _distance and not _prev_cell:
if solution[i][0] == dst: # found destination point start pathsearch
_distance = solution[i][1] - 1
_prev_cell = solution[i][0]
else:
if _distance == solution[i][1] and checkAdjacent(solution[i][0], _prev_cell): # if correct distance and if adjacent cell
_solution_path.append(solution[i][0])
_distance -= 1
_prev_cell = solution[i][0]
return _solution_path
def drawSolution(maze: list, src: list, dst: list, solutionpath: list):
"""draw the start- and endpoint as well as the solution
0 = wall
1 = cell
2 = path
3 = start- endpoint
Args:
maze (list): 2 dimensional array of the maze
src (list): y,x coordinates of the startpoint
dst (list): y,x coordinates of the endpoint
solutionpath (list): array of points of the solution
Returns:
list: 2d array of the maze including solution
"""
maze_tmp = maze.copy()
# draw solution
for point in solutionpath:
maze_tmp[point[0]][point[1]] = 2
# draw start and endpoint
maze_tmp[src[0]][src[1]] = 3
maze_tmp[dst[0]][dst[1]] = 3
return maze_tmp
def findEmptyCell(maze: list, corner: int):
"""find empty cell in cell starting at a corner
Args:
maze (list): maze to search through
corner (int): where to start (0=bottomleft, 1=topleft, 2=topright, 3=bottomright)
Returns:
list: row,col coordinates of the first empty cell
"""
maze_rows = len(maze)
maze_cols = len(maze[0])
if corner == 0:
range_rows = range(0, maze_rows-1, 1)
range_cols = range(0, maze_cols-1, 1)
elif corner == 1:
range_rows = range(0, maze_rows-1, 1)
range_cols = range(maze_cols-1, 0, -1)
elif corner == 2:
range_rows = range(maze_rows-1, 0, -1)
range_cols = range(maze_cols-1, 0, -1)
else:
range_rows = range(maze_rows-1, 0, -1)
range_cols = range(0, maze_cols-1, 1)
# find empty cell
for row in range_rows:
for col in range_cols:
if maze[row][col] == 1: # valid cell found
return [row, col]
Test¶
no_solution = True
while no_solution:
# generate maze with function from 008 notebook
size = {'x': 80, 'y': 40}
maze = generateMaze(size['x'], size['y'])
maze = createBorder(maze)
# get maze size
maze_rows = len(maze)
maze_cols = len(maze[0])
# find empty cell in topleft corner
src = findEmptyCell(maze, 0)
# find empty cell in bottomright corner
dst = findEmptyCell(maze, 2)
print("Maze Size : {}x{}".format(maze_cols, maze_rows))
print("Source Cell is : {}".format(src))
print("Destination Cell is : {}".format(dst))
# execute lees algorithms
(solution, dist) = bfsLee(maze, src, dst)
# draw points and solution
if dist != -1:
no_solution = False
path = getSolution(src, dst, solution)
print("Length of the Shortest Path is", dist)
maze_solved = drawSolution(maze, src, dst, path)
else:
#no_solution = False##
print("No solution exists")
clear_output(wait=True)
Maze Size : 81x41 Source Cell is : [1, 2] Destination Cell is : [39, 78] Length of the Shortest Path is 178
output_notebook()
plot = figure(x_range=(0, 1), y_range=(0, 1),
plot_height=maze_rows*10, plot_width=maze_cols*10)
plot.axis.visible = False
plot.outline_line_color = '#ffffff'
plot.image([maze_solved], x=0, y=0, dw=1, dh=1, palette=['#228b22', '#ffffff', '#add8e6', '#ff7f7f'])
show(plot)