Prime numbers with Eratosthenes sieve¶

Sieve of Eratosthenes is an ancien greek algorithm for finding all prime numbers up to any given limit.

A prime number is natural number that has exactly two distinct natural numbers divisors; the number 1 and itself.

The first prime numbers are

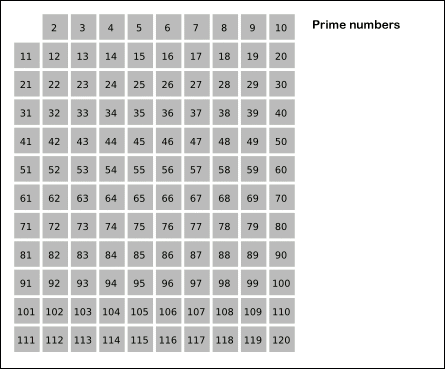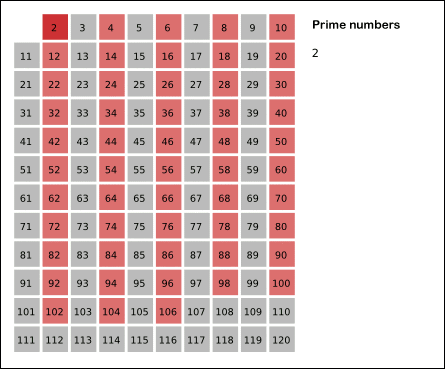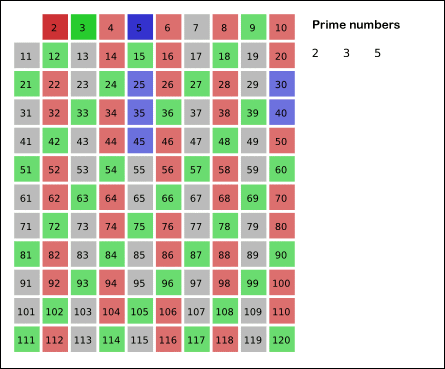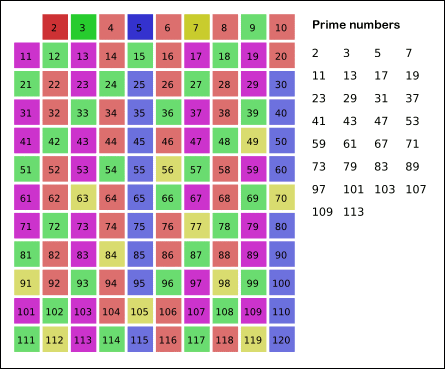
$$ 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113 $$

Solution¶

To find all the prime numbers less than or equal to a given integer $n$ by Eratosthenes' method:

1. Create a list of consecutive integers from $2$ through $n$: $(2, 3, 4, ..., n)$.
2. Initially, let $p$ equal 2, the smallest prime number.
3. Enumerate the multiples of $p$ by counting in increments of $p$ from $2p$ to $n$, and mark them in the list (these will be $2p, 3p, 4p, ...;$ the $p$ itself should not be marked).
4. Find the smallest number in the list greater than $p$ that is not marked. If there was no such number, stop. Otherwise, let $p$ now equal this new number (which is the next prime), and repeat from step 3.
5. When the algorithm terminates, the numbers remaining not marked in the list are all the primes below $n$.

Figure 1: Animation Sieve of Eratosthenes Source: Wikipedia

Imports¶

In [1]:

import numpy as np

import numpy as np

Algorithm¶

In [10]:

def seive_of_eratosthenes(n: int = 2):
  """Algorithm to get all Prime numbers up to the value n

  Args:
      n (int, optional): End number for the prime calculations. Defaults to 2.

  Returns:
      list: list of all primenumber upto n
  """
  # create empty array
  _is_prime = [True for i in range(n + 1)]
  # 0 and 1 are not primes
  _is_prime[0] = _is_prime[1] = False
  p = 2
  while (p * p <= n):
    # If prime[p] is not changed, then it is a prime
    if (_is_prime[p] == True):
      # Update all multiples of p
      for i in range(p ** 2, n + 1, p):
        _is_prime[i] = False
    p += 1
  return _is_prime


def print_primenumbers(is_prime: list):
  """Print all prime numbers indicated on a boolean list

  Args:
      is_prime (list): list of boolean indicating of the number is a prime
  """
  print("Following are the prime numbers smaller than {}".format(len(is_prime)))
  for p in range(len(is_prime)):
    if is_prime[p]:
      print(p, end=' ')

def seive_of_eratosthenes(n: int = 2): """Algorithm to get all Prime numbers up to the value n Args: n (int, optional): End number for the prime calculations. Defaults to 2. Returns: list: list of all primenumber upto n """ # create empty array _is_prime = [True for i in range(n + 1)] # 0 and 1 are not primes _is_prime[0] = _is_prime[1] = False p = 2 while (p * p <= n): # If prime[p] is not changed, then it is a prime if (_is_prime[p] == True): # Update all multiples of p for i in range(p ** 2, n + 1, p): _is_prime[i] = False p += 1 return _is_prime def print_primenumbers(is_prime: list): """Print all prime numbers indicated on a boolean list Args: is_prime (list): list of boolean indicating of the number is a prime """ print("Following are the prime numbers smaller than {}".format(len(is_prime))) for p in range(len(is_prime)): if is_prime[p]: print(p, end=' ')

Test¶

In [13]:

is_prime = seive_of_eratosthenes(120)
print_primenumbers(is_prime)

is_prime = seive_of_eratosthenes(120) print_primenumbers(is_prime)

Following are the prime numbers smaller than 121
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113